- Simple linear regression
: Classification의 목적은 class(y의 label)를 맞추는 것이고,
Regression 또한 y를 예측하는 것은 중요하나 실수 값이므로 완벽하게 예측하기가 불가능합니다.
따라서 Regression은 어떤 변수가 어느정도의 영향력으로 y에 영향을 미치는 여부를 예측 값 만큼 중요시 합니다.
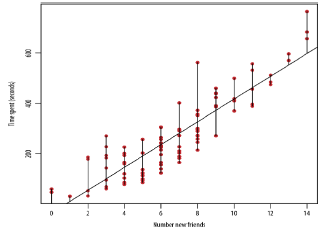
: Find a linear line that best fits the data points (x 1 ,y 1 ), (x 2 ,y 2 ), ..., (x n ,y n)

: 주어진 여러개의 line 중에서 특정 line에 의해 예측한 y 값과 실제 y 값의 차이를 최소화 하는 line을 찾는다.

- For each training data (Xi , Yi)
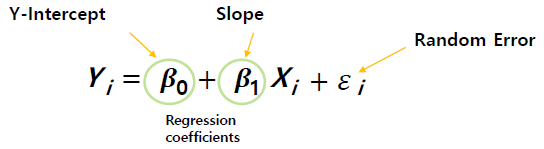
: 일반적으로
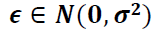
- Least squares (최소 제곱법)
: "최적 적합"은 실제 Y 값과 예측 Y 값의 차이가 최소임을 의미합니다.
잔차 제곱합을 최소화하는 계수 찾기입니다.
- Estimating model parameter
: 훈련 데이터 => n 개의 샘플
목표 => 실제 목표와 예상 목표 간의 차이 최소화
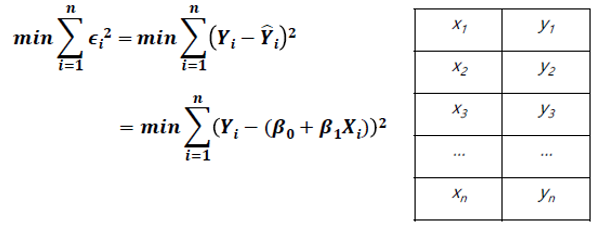
1. 최소 제곱 추정
: 다음 목적 함수 (Sum of Squared Errors, SSE)를 최소화하는 β 0, β 1 찾기
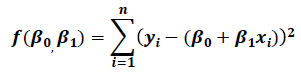
: 2 차 다항식
: 각 계수에 대한 f의 미분을 취합니다.
이후 계수를 얻는 방법?
: 볼록함수 (볼록 함수는 임의의 두 점을 이은 할선이 두 점을 이은 곡선보다 위에 있는 함수입니다.
엄밀히 말하면, x, y과 [0,1] 사이의 값 t에 대해 f\leq tf+f(y) 가 항상 성립하는 함수 f를 가리킵니다.)
: 고유 최소 포인트
2. 매개 변수의 유도
: 최소 제곱 (LS) : 제곱 오차 최소화
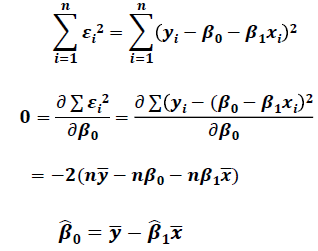
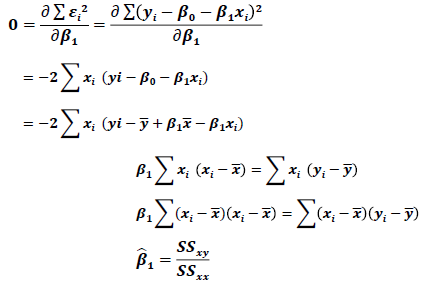
=> β0로 미분한 값입니다.
=> ∑ 기호를 제거하고 - 기호가 들어가는 평균으로 표현하였습니다.
3. 계수 방정식
: Prediction equation
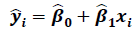
: Sample slope (기울기)

: Sample Y - intercept (y 절편)
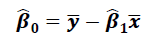
=> 위 값들이 linear regression을 학습한 결과물입니다.
- Multiple Linear Regression
: Fit a linear equation between a dependent variable Y and a set of predictors X=(X 1 , …, X p)
(종속 변수 Y와 예측 변수 집합 X = (X 1,…, X p) 사이에 선형 방정식 적합)
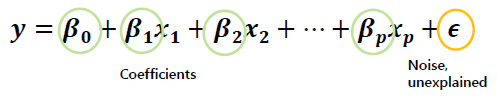
: Parameter 측정
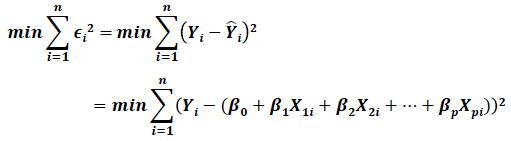
: feature의 수가 늘어나면 역행렬이 존재하지 않을 수 있거나 계산하기 어려울 수 있다.
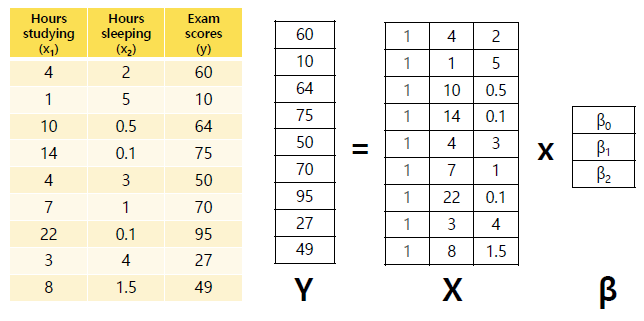
: 제곱 오차의 합을 최소화하는 β 값 선택
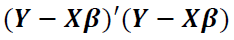
: β의 최소 제곱 추정치
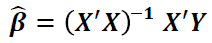
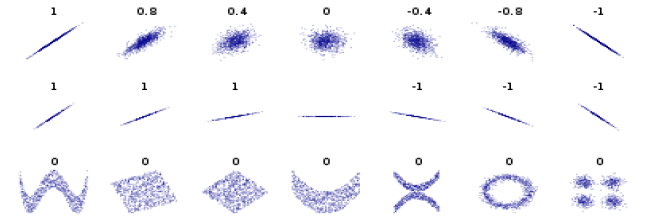
- Pearson’s Correlation coefficient (피어슨의 상관 계수)
: x, y의 선형 정도를 측정
값은 +1에서 -1 사이의 값을 가집니다. (값이 0일 경우 상관 관계가 없습니다.)
기울기의 값이 아니라 완벽한 선형 관계를 가지면 1의 값을 가집니다.니
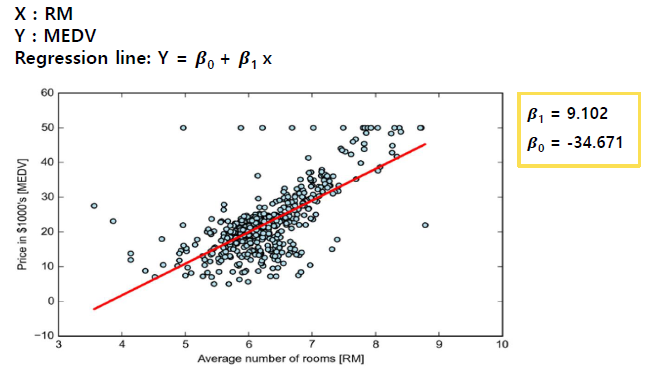
- 일반적인 최소 제곱 법 (OLS)에 의한 모델 피팅
: linear regression 으로 얻을 수 있는 값은 x 값에 따라 예측할 수 있는 y 값들의 평균 정도로 해석하는 것이 좋습니다.니
- Model Assumptions (모델 가정)
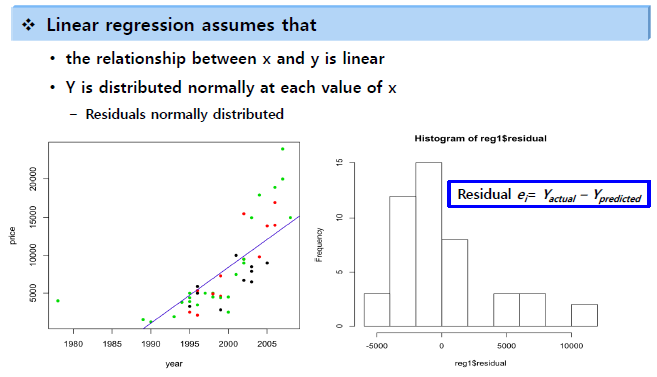
- Performance measure (성능 측정)
: linear regression 평가 지표

: R^2는 내 모델에 의해서 분산이 얼마나 줄어드는지 확인합니다.
Overfit을 잘 반영하지 못하는 특색이 있어서 약간 변형한 것이 R^2 adj 모델입니다.
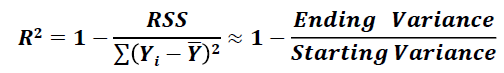
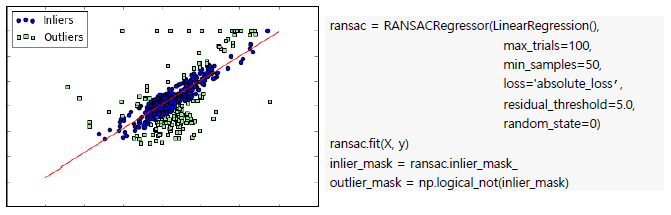
- Robust regression
: linear regression 은 평균과 관련이 있기도 해서 outlier 에 굉장히 민감합니다.
Robust regression은 outlier 을 버리고 중요한 지표만 뽑아서 사용하는 방식입니다.
- Modeling nonlinear regression
: 관계가 선형이 아닐 경우 비선형인 2차, 3차 고차 다항식 사용합니다.
사용시 model이 overfitting 하지 않는지 확인하여야 합니다.

: Feature에 대해 transformation 진행

아주대학교 정보통신대학원 손경아 교수님의 기계학습 및 데이터 마이닝 강의를 바탕으로 작성하였습니다.
학습 목적으로 포스팅 합니다.
'Machine Learning' 카테고리의 다른 글
| Logistic regression (0) | 2020.09.29 |
|---|---|
| Model selection (1) | 2020.09.29 |
| Ensemble method (0) | 2020.09.19 |
| Performance Metrics (1) | 2020.09.17 |
| Evaluation (0) | 2020.09.17 |