- Confusion Matrix (오차행렬)
: Confision Matrix (오차행렬) 이란,
Traning을 통한 Prediction의 성능을 측정하기 위해 예측한 Value와 실제 Value의 값을 비교한 표입니다.
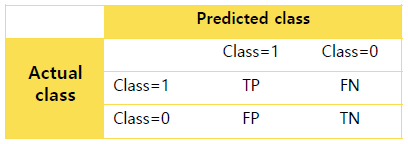
- True Positive (TP): Correctly classified as the class of interest
모델은 1의 값을 예측하였고, 실제 값도 1인 경우 (예측 값: 1, 실제 값: 1)
- False Negative (FN): Incorrectly classified as not the class of interest
모델은 0의 값을 예측하였지만, 실제 값은 1인 경우 (예측 값: 0, 실제 값: 1)
- False Positive (FP): Incorrectly classified as the class of interest
모델은 1의 값을 예측하였지만, 실제 값은 0인 경우 (예측 값: 1, 실제 값: 0)
- True Negative (TN): Correctly classified as not the class of interest
모델은 0의 값을 예측하였고, 실제 값도 0인 경우 (예측 값: 0, 실제 값: 0)
- Accuracy (정확성) 계산
: 클래스 중에서 모델이 실제 값을 정확하게 예측하였을 경우를 계산해 구합니다.
아래에서 8개의 클래스에 대해 실제 값이 0이든 1이든, 이를 정확하게 예측한 5개의 클래스를 계산에 62.5%의 Accuracy를 구할 수 있습니다.

: Error 값은 1-Accuracy의 값으로 구할 수 있습니다.
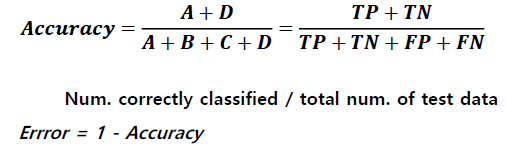
- Accuracy (정확성)의 한계
: 다음과 같은 극단적인 Case의 경우 Accuracy에는 한계가 있습니다.
- Case. 이진 분류 (분류기가 0과 1의 값의 분류 없이, 모든 값을 0으로만 예측하더하도 99.9%의 Accuracy를 가집니다.)
· 클래스 0의 수 => 9990개
· 클래스 1의 수 => 10개
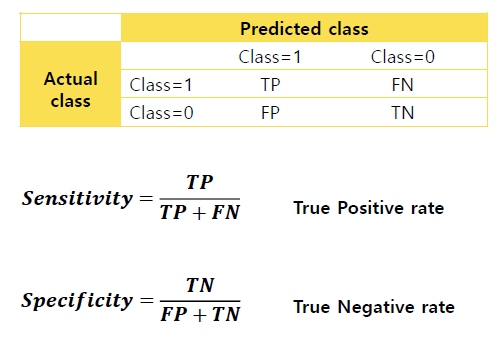
- Sensitivity (민감도) & Specificity (특이도) - Trade off 관계
: Sensitivity (민감도)는 질병이 실제로 있고, Test 결과에서도 질병이 있다고 판단하는 비율입니다.
Specificity (특이도)는 질병이 실제로 없고, Test 결과에서도 질병이 없다고 판단하는 비율입니다.
민감도가 높다는 것은 질병이 있지만, Test에서는 질병이 없다고 놓친 비율이 적다는 것은 의미하고
반대로, 특이도가 높다는 것은 질병이 없지만, Test에서는 질병이 있다고 잘못 측정한 비율이 적다는 의미로도 표현이 가능합니다.
민감도와 특이도는 Trade off (상반) 관계에 있습니다.
- Precision(정밀도) & Recall(재현율)
: Precision (정밀도)란, 모델이 True라고 분류한 것 중에서 실제 True인 것의 비율입니다
Recall (재현율)이란, 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율입니다.

- F1 score (조화평균)
: F1 score는 precision과 recall을 조합하여 하나의 통계치를 반환합니다. 여기서 일반적인 평균이 아닌 조화 평균을 계산하였는데,
그 이유는 precision과 recall이 0 에 가까울수록 F1 score도 동일하게 낮은 값을 갖도록 하기 위함입니다.

- ROC curve (Receiver Operating Characteristic) curve
: 알고리즘의 Hyper-parameter 혹은 Threshold 를 바꿔가며 그래프로 만든 것 입니다.
(ROC curve plots (1-specificity) (or FP rate) on the x-axis against sensitivity (or TP rate) on the y-axis)
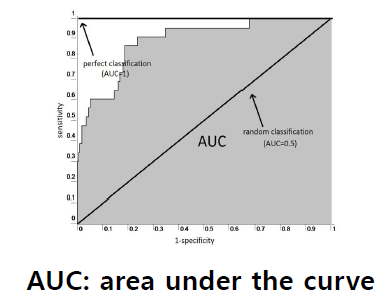
여러 임계값들을 기준으로 Recall-Fallout의 변화를 시각화한 것입니다. Fallout은 실제 False인 data 중에서 모델이 True로 분류한,
그리고 Recall은 실제 True인 data 중에서 모델이 True로 분류한 비율을 나타낸 지표로써,
이 두 지표를 각각 x, y의 축으로 놓고 그려지는 그래프를 해석합니다.
ROC curve는 그래프이기 때문에 명확한 수치로써 비교하기가 어렵습니다. 따라서 그래프 아래의 면적값을 이용합니다.
이것이 바로 AUC(Area Under Curve)입니다. 최대값은 1이며 좋은 모델(즉, Fall-out에 비해 Recall 값이 클수록) 1에 가까운 값이 나옵니다.
: ROC curve 구성 순서
1. 각 테스트 인스턴스 P (+ | A)에 대한 앞쪽 확률을 생성하는 분류기를 사용합니다.
2. 내림차순으로 P (+ | A)에 따라 인스턴스 정렬
3. P (+ | A)의 각 고유 값에 임계 값 적용
4. 각 임계 값에서 TP, FP, TN, FN 계산
5. TP 비율, FP 비율 계산

- Micro-averaging
: 전체의 값들의 평균 개념이며 마이크로 평균(Micro-average)이라고 불리는 방법입니다.
각 샘플에 동일한 가중치를 적용하려는 경우 유용합니다.


계산과정.
4+2+6 = 12 correctly predicted sample (TP = 12)
FP = 6+3+1+0+1+2 = 13
Micro-precision = 12/(12+13) = 48.0
Micro-recall = 12/(12+13) = 48.0
- Macro-averaging
: 평균들의 평균 개념이며 매크로 평균(Macro-average)이라고 불리는 방법입니다.
Macro 는 사이즈가 크건 작건 하나의 precision 으로 묶어서, micro 는 TP/FP 가 많으므로 영향을 많이 미칩니다.
전체 성능을 평가하기 위해 모든 클래스에 동일한 가중치를 부여합니다.
Sample에 대해 동일한 weight를 주는 것이 아닌, Class 별로 똑같은 weight을 부여합니다.
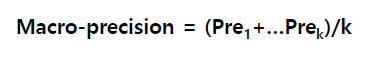

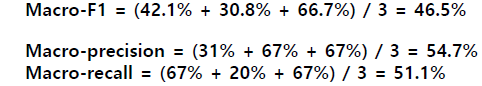
- Weighted macro-average
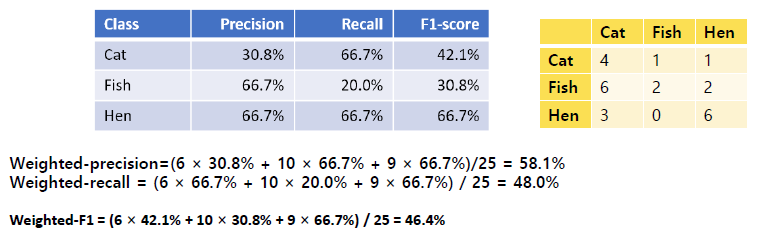
: 실제 인스턴스 수에 따라 각 클래스의 점수에 가중치를 부여하여 계산하는 방법입니다.
이는 클래스 불균형을 다룰 때 유용합니다.
- 클래스의 불균형 문제
: 다른 클래스보다 훨씬 많은 샘플이 있을 경우.
실제 데이터 작업시 일반적으로 발생하는 문제입니다. (ex. 스팸 필터링, 사기 탐지, 질병 검사)
: 해결방안
1. minority class에 대해 잘못 예측하면, 더 많은 penalty를 줍니다.
2. minority class에 더 많은 중복을 하여, sampling, majority class 를 줄이든지 시뮬레이션 데이터를 생성하여 사용합니다.
3. but, universal한 해결책은 없으므로 상황에 따라 판단하여 사용하도록 합니다.
아주대학교 정보통신대학원 손경아 교수님의 기계학습 및 데이터 마이닝 강의를 바탕으로 작성하였습니다.
학습 목적으로 포스팅 합니다.
'Machine Learning' 카테고리의 다른 글
| Regression (0) | 2020.09.27 |
|---|---|
| Ensemble method (0) | 2020.09.19 |
| Evaluation (0) | 2020.09.17 |
| Decision Tree (0) | 2020.09.12 |
| Support Vertor Machine (0) | 2020.09.12 |