- Support Vertor Machine
SVM은 기계 학습의 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델이며, 주로 분류와 회귀 분석을 위해 사용합니다.
두 카테고리 중 어느 하나에 속한 데이터의 집합이 주어졌을 때, SVM 알고리즘은 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가
어느 카테고리에 속할지 판단하는 비확률적 이진 선형 분류 모델을 만듭니다.
만들어진 분류 모델은 데이터가 사상된 공간에서 경계로 표현되는데 SVM 알고리즘은 그 중 가장 큰 폭을 가진 경계를 찾는 알고리즘입니다.

- SVM (Support Vector Machine)은 분류를 위한 학습 기술을 제공
: 이론적으로 우아함 · 계산 효율성 · 많은 큰 실제 문제에 매우 효과적입니다.
: 입력 공간과 비선형적으로 관련된 고차원 특성 공간에서 단순한 기하학적 해석을 가집니다.
: 커널을 사용하면 모든 계산이 간단해집니다.
- Linear SVM: Separable case
(N 개의 훈련 샘플 (Xi, Yi), i = 1, ..., N으로 구성된 이진 분류)
: 선형 결정 경계
결정 경계는 두 클래스의 데이터를 분류하는 기준이 되는 경계로,
Linear SVM의 결정 경계는 데이터의 feature 차원의 초평면(Hyperplane)이 됩니다.

: 선형 분류
기계 학습 분야에서 통계적 분류는 개체의 속성을 이용하여 그 개체가 속하는 그룹, 또는 클래스를 판별하는 것을 목표로 합니다.
선형 분류에서는 주어진 속성의 선형결합을 바탕으로 분류를 수행합니다.
개체의 속성은 피쳐 값이라고 부르기도 하는데, 보통 피쳐 벡터라는 벡터 형태로 제공합니다.

: 선형 SVM
새로운 데이터가 들어왔을 때, 해당 데이터를 구분시켜 줄 기준이 되는 선을 서포트 벡터라고 합니다.
두 개의 그룹을 구분하는 일정한 거리는 마진 (Margin)이라고 하며, 마진이 최대값을 가질 때의 중간 경계선을 결정 경계라고 합니다.
SVM은 각 그룹이 최대로 떨어질 수 있는 거리 (최대 마진)를 찾고, 해당 거리의 중간지점 (결정 경계)으로 그룹을 구분하는 기법입니다.
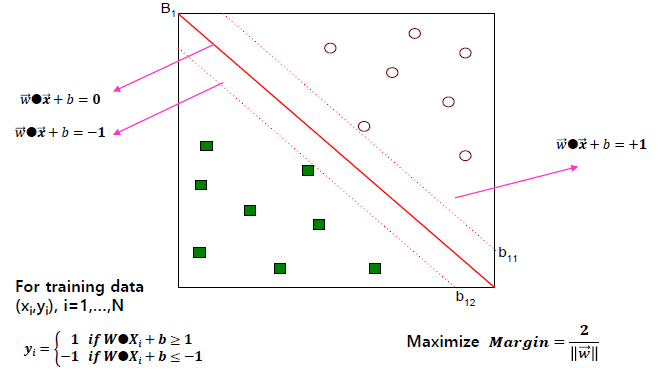
- Learning linear SVM
1. Training 단계: 훈련 데이터에서 매개 변수 w 및 b 추정
: Objective: maximize margin (마진 최대화)

2. Test 단계 (Test 단계에서의 계산량이 적다.)
: 결정 경계 (w, b)의 매개 변수가 발견되면 테스트 인스턴스 z는 다음과 같이 분류됩니다.
f(z) = 1 if w·z + b ≥ 0
f(z) = -1 otherwise
- Linear SVM: non-separable case
: Relax the constraints
· W·Xi+b ≥ 1-ξ if yi=1
· W·Xi+b ≤ 1+ξ if yi=-1
: 일부 점은 선 사이의 영역에있을 수 있습니다.

- Nonlinear SVM
인스턴스를 분리하여 선형 경계를 사용할 수 있도록 데이터를 새 공간으로 변환합니다.
고차원 공간에서의 계산은 비용이 많이들 수 있지만, Kernel Trick 기법을 사용하여 문제를 해결합니다.
1. Training 단계
· subject to -> yi(W·Φ(Xi)+b) ≥ 1, i=1,...,N
2. Test 단계: for a new instance z,
· f(z) = 1 if W·Φ(z)+b ≥ 0
· f(z) = -1 otherwise
- Kernel trick
커널을 도입하게 되면 연산량이 폭증하게 됩니다.
모든 관측치에 대해 고차원으로 매핑하고 이를 다시 내적(inner product)해야 하기 때문입니다.
고차원 매핑과 내적을 한번에 진행하기 위해 도입된 것이 바로 커널(Kernel)입니다.


=> 변형 된 공간에서의 내적을 원래 공간에서의 유사성으로 표현
- 커널 함수는 일부 고차원 공간에서 두 입력 벡터 간의 내적 (dot product)으로 표현될 수 있습니다.
- 커널 함수를 사용하여 내적을 계산하는 것은 변형 된 속성을 사용하는 것보다 훨씬 저렴합니다.
- 매핑 함수 Φ의 정확한 형태를 알 필요는 없습니다.
- SVM summary
- 효율적인 알고리즘을 사용할 수있는 볼록 최적화 문제
- 결정 경계의 마진 최대화
- 속성 고차원 공간 및 커널 트릭으로의 변환
- 사용자는 커널 함수 유형 및 여유 변수에 대한 비용 함수 C와 같은 다른 매개 변수를 계속 제공해야함
- 이진 분류 용. 다중 클래스 문제로 확장 가능
아주대학교 정보통신대학원 손경아 교수님의 기계학습 및 데이터 마이닝 강의를 바탕으로 작성하였습니다.
학습 목적으로 포스팅 합니다.
'Machine Learning' 카테고리의 다른 글
| Evaluation (0) | 2020.09.17 |
|---|---|
| Decision Tree (0) | 2020.09.12 |
| KNN algorithm (0) | 2020.09.12 |
| 탐색적 데이터 분석 (Exploratory Data Analysis) (0) | 2020.09.05 |
| 데이터 및 데이터 품질 (0) | 2020.09.05 |