- 일반적인 기계 학습 Workflows
: Streaming workflows with pipeline

1. Input preprocessing
· feature scaling
· standardization (표준화)
2. Feature selection, extraction => Dimension Reduction (차원 축소)
· PCA (주성분 분석)
· embedding
3. Model Fitting (학습)
Testing (평가)
- Combining transformers (변환기) and estimators (학습 및 추론) in a pipeline
: model의 fitting 및 training and datasets 변환을 분리하는 것보다 두 단계를 chain화 하여,
쉽게 구현할 수 있는 scikit-learn Pipeline 사용
- 모델 성능 평가
: 학습에 사용하지 않았던 새로운 데이터를 통해 모델의 성능을 평가하는 과정
: Model이 너무 간단한 경우 (underfitting (high bias): training error가 큼)
=> 모델이 너무 단순해서 데이터의 내재된 구조를 학습하지 못할 때 발생
: Model이 너무 복잡한 경우 (overfitting (high variance): training error는 작지만, test error가 큼)
=> 모델이 훈련 데이터에 너무 잘 맞지만 일반성이 떨어진다는 의미
: bais와 variance는 tradeoff (상반) 관계에 있기 때문에,
Model을 신중하게 평가 후 결정해야 함
: Underfitting and Overfitting 비교

- Validation (검증)
: Internal Validation
현재 가진 데이터 안에서 평가
: External Validation
외부에서 데이터를 가져와 완전히 새로운 데이터를 통해 평가
: Cross Validation
가진 데이터를 잘 나누어 평가 (Training - Test)
- Cross Validation (교차 검증)
: 모델을 생성하고 예측했다고 해서 모델이 좋은 예측을 하는 것은 아닙니다. 훈련 시에는 좋은 점수를 얻었지만,
훈련에서 너무 안 좋은 점수를 얻는 경우가 생깁니다.
이를 과적합(Overfitting)이라고 하는데 ,이를 피하기 위해서 훈련 데이터 세트 전체를 한 번에 훈련시키지 않고,
일부를 남겨두고 테스트하는 것에 사용합니다. 이러한 방법을 Cross Validation (교차 검증) 이라고 합니다.
데이터를 분할하고 모델을 학습시킬 때, 다양한 매개변수를 필요로 합니다.
하지만 각각의 최적의 매개변수를 찾는 일은 아주 힘듭니다. 최고의 매개변수를 찾기 위한 여러 방법 중 하나가 바로 교차 검증입니다.
: Cross Validation의 사용
1. Over-fitting 방지
2. 다른 알고리즘들과의 비교
3. 최적의 hyper-parameter setting을 선택하기 위해 사용
4. 일반화 가능성을 설명할 필요가 있을 경우
- Holdout (or Test-set) Validation
: Holdout은 데이터 셋을 Train set과 Test set 두 세트로 나누는 과정을 의미합니다.
보통 데이터셋을 8 : 2로 설정하고 사용하지만, 경우에 따라 5 : 5, 7 : 3, 9 : 1 비율로도 사용합니다.
- ex) Training set (50%) + Test set (50%)
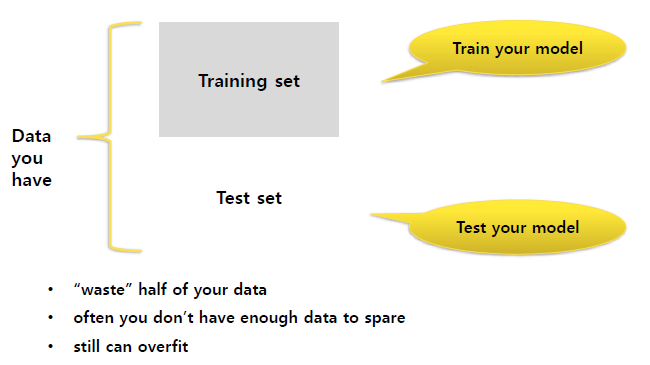
- Train / Validation / Test split
: Holdout Validation 처럼 Training set과 Test set을 극단적으로 나누지 안고 세부분으로 나누어 사용하는 방법입니다.
Hyper-parameters를 평가하기 위해 Training set를 Training set과 Validation set으로 나눈 후 Test set으로 성능 평가를 진행합니다.
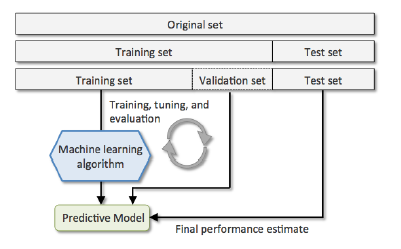
- K-fold cross validation
: K-fold cross validation 방법은 가장 일반적으로 사용되는 교차 검증 방법입니다.
데이터를 k개의 데이터 폴드로 분할하고, 각 Iteration마다 test set을 다르게 할당하여 총 k개의 데이터 폴드 세트를 구성합니다.
따라서 모델을 학습 및 훈련하는데 총 k번의 Iteration이 필요한 것이 특징입니다.
각 데이터 폴드 세트에 대해서 나온 검증 결과들을 평균내어 최종적인 검증 결과를 도출하는 것이 일반적인 과정입니다.
: K-fold cross validation의 특징
1. holdout method를 개선
2. 데이터를 k개의 subsets으로 나누고, holdout method를 k번 반복
- Algorithm selection with nested cross-validation
: Nested CV는 Outer Loop와 Inner Loop로 구성되어 있습니다.
outer loop에는 기존 validation set을 나눈 것 대신에 test set을 다양하게 나누어서 fold를 구성했습니다.
결국 outer loop에서는 test set에 대한 평가를 inner loop에서는 각 폴드의 최적 파라미터를 튜닝하는 것이 목적입니다.
1. 다른 알고리즘을 비교할 때 유용합니다.
2. Outer loop to split data into training and test folds (알고리즘 별 성능 설정)
3. Inner loop for tuning the parameter using k-fold cv (알고리즘 별 최적화 hyper-parameter 설정)
4. 1개를 Test set으로 사용, k-1개를 Training set으로 사용
5. k번 반복한 것의 평균으로 평가
6. 가장 좋은 성능의 hyper-parameter를 정한 후 다시 전체 모델에 대해 최종학습 진행
ex. oo oo oo oo oo => ramdomly divide
xx oo oo oo oo => E1
oo xx oo oo oo => E2
oo oo xx oo oo => E3
oo oo oo xx oo => E4
oo oo oo oo xx => E5
=> (E1+E2+E3+E4+E5)/5
(Whichever model class gave best CV score: train it with all the data, and that's the predictive model you will use)
- K-fold CV advantages
: 각각의 data point들이 test set에 정확하게 1번 들어가고, training set에는 k-1번씩 들어감
(Lower-variance estimate than the holdout metho)
: 전형적으로 10-fold (or 5-fold)를 CV 사용합니다.
- Improvement
: Stratfied K-fold CV (층화 K-fold CV)
(Slight improvement over the standard K-fold CV, especially in cases of unequal class proportions)
: The class label proportions are preserved in each fold
- Leave-one-out CV
: Leave-one-out cross validation은 줄여서 LOOCV라고도 불리우며, leave-p-out cross validation에서 p=1일 때의 경우입니다.
leave-p-out cross validation 보다 계산 시간에 대한 부담은 줄어들고, 더 좋은 결과를 얻을 수 있기 때문에 더욱 선호됩니다.
검증에 사용되는 test set의 갯수가 적은 만큼 모델 훈련에 사용되는 데이터의 갯수는 늘어납니다.
모델 검증에 희생되는 데이터의 갯수가 단 하나이기 때문에, 나머지 모든 데이터를 모델 훈련에 사용할 수 있다는 것이 장점입니다.
: Special case of K-fold CV
: K = n (the number of training samples)
: Recommended for working with very small datasets
ex. oooooooooo : o-train sample / x-validation sample
xooooooooo -> Accuracy (1)
oxoooooooo -> Accuracy (2)
...
ooooooooox -> Accuracy (n)
=> Final accuracy = (Accuracy (1)+...+Accuracy(n)) / n
- Cross Validation 종류 비교

- 편향 및 분산 문제

아주대학교 정보통신대학원 손경아 교수님의 기계학습 및 데이터 마이닝 강의를 바탕으로 작성하였습니다.
학습 목적으로 포스팅 합니다.
'Machine Learning' 카테고리의 다른 글
| Ensemble method (0) | 2020.09.19 |
|---|---|
| Performance Metrics (1) | 2020.09.17 |
| Decision Tree (0) | 2020.09.12 |
| Support Vertor Machine (0) | 2020.09.12 |
| KNN algorithm (0) | 2020.09.12 |