- 최소 제곱 회귀 추정치 개선
: 최소 제곱 원리(least square principle)는 제곱 오차의 합을 최소화하여 계수를 효과적으로 선택할 수 있는 방법입니다.
즉, 최소화하는 값을 선택합니다.
오차를 제곱하여 더한 양의 최소값을 나타내기 때문에 이것을 최소 제곱(least square) 추정이라고 부릅니다.
계수의 가장 좋은 추정치를 찾는 것을, 종종 모델을 데이터에 맞춘다 고 부르거나,
때때로 모델을 학습(learning) 시키거나 훈련(training) 시킨다고 부릅니다.
1. Prediction Accuracy (예측 정확도)
최소 제곱 추정값은 특히 Y와 X 간의 관계가 선형이고 관측치 수 n이 예측 변수의 수 p보다 훨씬 클 때 상대적으로 편향이 낮고 변동성이 낮습니다.
그러나 n <p 일 때 최소 제곱 적합은 높은 분산을 가질 수 있으며 보이지 않는 관측치에 대해 과적 합 및 잘못된 추정을 초래할 수 있습니다.
그리고 𝒏≈𝒑 일 때 최소 제곱 적합도의 변동성은 극적으로 증가하고 이러한 추정값의 분산은 무한합니다.
=> 샘플이 충분히 많을 경우(p보다 n이 훨씬 클 경우) 문제가 없지만 반대의 경우 역행렬이 구해지지가 않고 overfit의 가능성이 있습니다.
2. Model Interpretability
모델에 많은 수의 변수 X가있을 때 일반적으로 Y에 거의 또는 전혀 영향을 미치지 않는 많은 변수가 있습니다.
이러한 변수를 모델에 남겨두면 "큰 그림", 즉 "중요한 영향"을보기가 더 어려워집니다.
중요하지 않은 변수를 제거 (즉, 계수를 0으로 설정)하면 모델을 해석하기가 더 쉽습니다.
=> 해석적인 측면에서 p를 줄이는 것이 좋습니다. noise로 인해 방해는 받는 경우가 있고, 중요하지 않은 변수를 먼저 버립니다.
: 해결책
1. 부분 집합 선택
반응 Y와 관련이 있다고 생각되는 모든 p 예측 변수 X의 하위 집합을 식별 한 다음이 하위 집합을 사용하여 모델을 피팅합니다.
2. 정규화 된 모델
추정 계수를 0으로 축소하는 것을 포함합니다. (E.g. Ridge regression and the Lasso )
3. 차원 축소
모든 p 예측 변수를 M <p 인 M 차원 공간에 투영 한 다음 선형 회귀 모델을 피팅합니다.
- 변수 선택
: 변수는 1000개 인데, sample은 50개일 경우는 modeling이 되지않는다.

- 간결한 모델 찾기
• More robust
• Higher predictive accuracy
• Parsimony (a.k.a. Occam’s razor): the simpler, the better
- Methods
• Exhaustive search
For p predictors, explore 2 p possibilities and choose the best
• Partial search
Forward, Backward, Stepwise
- Exhaustive Search (Best Subset Selection)
: 평가 된 예측 변수의 가능한 모든 하위 집합
가장 adjusted 하지만, 시간이 많이 걸리므로 큰 p에 대해서는 수행할 수 없습니다.

- Forward selection (전진 선택)
: 예측 변수없이 시작
: 하나씩 추가 (가장 기여도가 높은 항목 추가)
: 추가가 통계적으로 유의미하지 않으면 중지
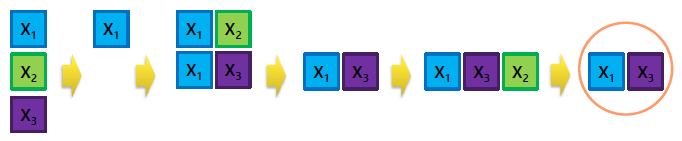
=> X1, X2, X3 하나씩 따로 평가 진행 후 가장 값이 좋았던 R^2를 가지는 모델을 선택 (X1)
=> R^2 값이 더이상 좋아지지 않을 때까지 진행
=> X1 이 먼저 뽑혔기 때문에 missing 되는 case들이 존재함
- Backward elimination (후진 제거)
: 모든 예측 자로 시작
: 유용하지 않은 예측 변수를 하나씩 연속적으로 제거
: 나머지 모든 예측 변수가 통계적으로 유의미한 기여를하면 중지
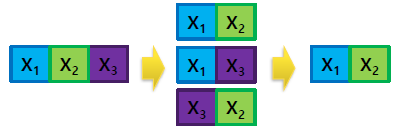
=> 전체의 모델에 대해서 평가 후 하나씩 제거하며 진행
- Stepwise selection (단계 선택)
: 역방향 제거 (또는 순방향 선택)
: 각 단계를 제외하고 유의 한 예측 변수를 다시 추가하거나 중요하지 않은 예측 변수를 삭제하는 것도 고려
=> 위 Forward selection, Backward elimination의 경우 순서에 의해 전혀 고려되지 않는 점을 보완
=> 1번은 빼고, 1번은 더하는 식으로 평가진행
- R^2 vs. Subset Size
: RSS / R^2는 변수의 수가 증가함에 따라 항상 감소 / 증가하므로별로 유용하지 않습니다.
빨간색 선은 RSS 및 R^2에 따라 주어진 수의 예측 변수에 대해 최상의 모델을 추적합니다.
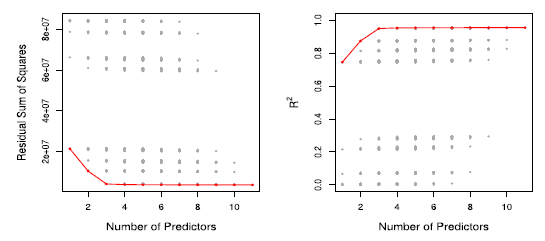
=> RSS는 training data에서의 error 값으로 R^2와 마찬가지로 변수의 수(p)가 증가할 수록 더 좋아지므로 model 선정에 도움이 되지 않음
=> 따라서 위 값을 기준으로 model을 선정 시 overfit의 위험성이 있으므로 선정하면 안됨
- Other Measures of Comparison (기타 비교 측정)정
: 다른 모델을 비교하기 위해 다른 접근 방식을 사용할 수 있습니다.
공통적으로 RSS를 기반으로 하되, 변수의 수가 증가할수록 패널티를 주는 방식으로 진행
• Adjusted R^2
• AIC (Akaike information criterion)
• BIC (Bayesian information criterion)
• Cp (equivalent to AIC for linear regression
=> 이러한 방법은 모델의 변수 수 (예 : 복잡성)에 대해 RSS에 페널티를 추가합니다.
=> None are perfect
- Choosing the optimal model (최적의 모델 선택)

- Ridge Regression
: Ridge Regression는 약간 다른 방정식을 사용합니다.

: 정리

=> p가 커져도 tuning parameter만 설정한 후 한번만 돌리면 됩니다.
=> n이 p 보다 작을 경우에도 안정적으로 구해집니다.
- LASSO’s Penalty Term
: The LASSO estimates the 𝜷′𝒔by minimizing the

=> Ridge Regression 와 달리 절대값의 합으로 패널티로 사용시 특정 coefficients 들은 정확하게 0이 됩니다.
=> 최적의 hyperparameter 설정이 필요하고, 무조건 변수가 많을 수록 성능이 좋은 것은 아닙니다.
=> hyperparameter 를 찾을 경우 로그 스케일로 찾는 것이 좋습니다.
- Sparse regression

아주대학교 정보통신대학원 손경아 교수님의 기계학습 및 데이터 마이닝 강의를 바탕으로 작성하였습니다.
학습 목적으로 포스팅 합니다.
'Machine Learning' 카테고리의 다른 글
| Neural network: perceptron (0) | 2020.10.01 |
|---|---|
| Logistic regression (0) | 2020.09.29 |
| Regression (0) | 2020.09.27 |
| Ensemble method (0) | 2020.09.19 |
| Performance Metrics (1) | 2020.09.17 |