- Linear Model (선형 모델)
: 일부 알고리즘은 런타임에 느립니다. ( e.g. K NN)
: 선형 모델은 학습과 런타임에 모두 매우 빠릅니다.
: 더 단순한 모델이 더 해석 가능합니다. (e.g. linear)
Example 1.
: 합격/불합격 예측
• 우리는 학생이 회계 시험에 합격할지 불합격할지 예측하고 싶습니다.
• Y (통과?) 변수는 범주 형 : 0 또는 1
• X 변수는 학생의 수학 시험 점수를 지정하는 숫자 값입니다.

=> 위의 경우 데이터의 경향성은 확실하지만 linear model을 사용하기에는 맞지 않음
=> 이처럼 categorical한 데이터에 대해서는 바로 linear regression을 진행하면 안됨
=> 이런 경우 아래의 Logistic Function 같이 y를 예측하는 것이 아니라 y가 1일 확률을 예측한다.
- 해결책: Logistic Function 사용
: Y를 예측하는 대신 P (Y = 1), 즉 학생이 시험에 합격 할 확률을 예측해 보겠습니다.
: 따라서 0과 1 사이의 출력을 제공하는 함수를 사용하여 P (Y = 1)를 모델링 할 수 있습니다.
: 로지스틱 회귀 사용
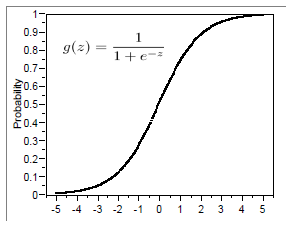
=> Logistic Function 의 output 은 각 클래스의 확률 값이다.
=> y 값 자체를 예측하는 것이 아니라 y가 1일 확률을 예측
- Simple Logistic Regression
: 로지스틱 회귀는 선형 회귀와 매우 유사합니다.
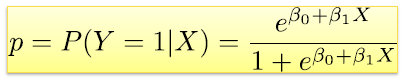
=> 어떤 값 x가 주어져 있을 때, y가 1이 될 확률
=> 모델을 해석하는 경우에도 사용이 가능하다.
Example 2.
: 성공 확률 (y=1)

Example 3.
: 데이터에 가장 적합한 곡선을 선택하고자 합니다.

=> 1번째 경우에 비해, 2번에 경우 β 값이 굉장히 작은 것을 확인할 수 있다.
=> β1을 해석하는 것이 기울기와 관련이 있다.
(0 = Y와 X간 관련이 없다. / 1 = X가 커지면 Y가 1일 확률이 커짐 / -1 = X가 커지면 Y가 1일 확률이 작아짐)
- Odds (오즈)
: Odds는 Probability의 또 다른 표현법이라고 볼수 있고,
어떠한 사건이 일어날 확률을 p라고 한다면 그 사건에 대한 odds는 p/(1−p)로 구할 수 있습니다.
또한, Odds는 도박 배팅이나 혹은 질병의 발병 확률을 표현할때 많이 사용됩니다.

: Log odds (logit) is linear in logistic regression

=> logistic regression는 Log odds를 linear하게 표현한 model입니다.
=> 위에서 linear 식이 0이되는 구간이 클래스가 1일 확률과 0일 확률이 같아지는 decision boundary가 됩니다.
Example 4

=> Intercept = y절편 / balance = 회귀계수
=> 0.0055가 정말 작아서 영향을 미치지 않는지, 중요한 값인지는 가설 검증을 통해서 확인
=> 실제로 0인데, 우연히 발견했을 확률은 P-value에 따라 0.0001이므로 실제로 의미가 있는 값이라고 판단 가능

=> 금액은 두배가 되었지만, 확률은 엄청 올라갔으므로 확률 자체에 대해 linear한 것은 아니다.
=> linear classifier 라고 하는 이유는 그 공간을 선형 직선으로 나누기 때문이다.
- Multiple Logistic Regression
: Multiple variables case

Example 5

=> balance와 student 값이 있을 경우 income 정보를 굳이 사용할 필요는 없다. P-value가 크기 때문이다.
=> student 일수록 불이행 정도가 떨어진다.
- An Apparent Contradiction!

=> simple과 multiple의 경향성이 서로 다르게 나올 수 있다.
=> balance과 income 정보가 없을 경우에 정보가 달라질 수 있다는 것을 나타낸다. 정보 사이에 서로 관계가 있다.
- Logistic Regression 모델의 결정 경계
: class가 1일 확률과 0일 확률이 동일해 지는 지점이 Decision boundary 이다.

=> logistic regression model의 확률 값 자체는 non-linear 이지만, Decision boundary를 보면 linear classifier 이다.
- Multi-class Classification
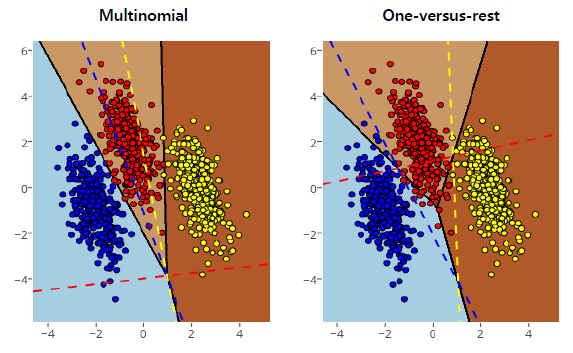
: Multinomial logistic regression (softmax regression)
: 클래스가 binary가 아닐 경우
: 클래스가 서로 겹치지 않을 때 사용하면 좋다. (하나의 sample이 하나의 class에만 영향을 미치는 경우)
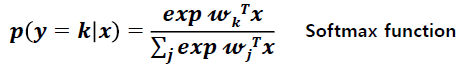
: Or, One versus Rest ( OvR , or OvA : one vs. all)
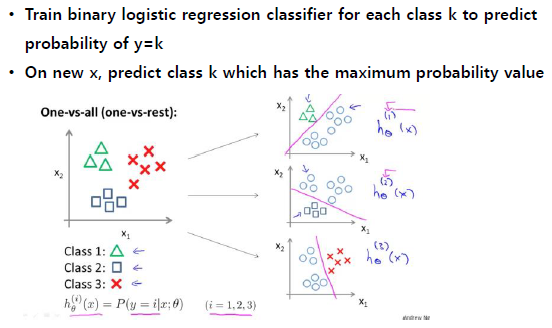
=> 각 sample에 대해서 확률 값이 가장 큰 클래스로 예측하는 방식
- Logistic Regression 모델 학습
: 선형 회귀의 경우보다 복잡
: 모델이 학습 세트 레이블을 최대한 재현 할 수 있도록 𝛽을 최적화해야합니다.
• 일반적으로 최대 가능성 추정 (MLE)의 수치 근사치로 수행
• 매우 큰 데이터 세트에서는 확률 적 경사 하강 법을 사용할 수 있습니다.

- 정규화된 Logistic Regression
: 정규화를 통해 모델 복잡성 조정
e.g. Add L2 penalty on the cost function
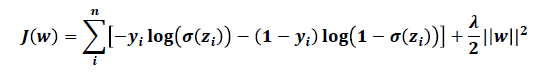
=> overfitting 문제를 해결하기 위해 penalty term을 넣는다.
아주대학교 정보통신대학원 손경아 교수님의 기계학습 및 데이터 마이닝 강의를 바탕으로 작성하였습니다.
학습 목적으로 포스팅 합니다.
'Machine Learning' 카테고리의 다른 글
| Artificial Neural network (0) | 2020.10.01 |
|---|---|
| Neural network: perceptron (0) | 2020.10.01 |
| Model selection (1) | 2020.09.29 |
| Regression (0) | 2020.09.27 |
| Ensemble method (0) | 2020.09.19 |