* 명제 논리의 한계
명제 논리(Propositional Logic)의 세계에서 사용할 수 있는 것은 명제 변수(Proposition Variable)와 이들을 연결하는 논리 연산자 뿐이다.
따라서 세상을 보다 잘 표현하기 위하여, 예를 로봇-7이 로봇-12 보다 오른 편에 있다는 객체들 간의 관계를 표현하기가 매우 어렵다.
이를 위하여는 모든 좌표에 대하여 일일이 오른 편에 있다는 명제 논리의 문장을 통하여 선언해야 하는,
사실상 경우의 수가 많으면 불가능하지만, 설혹 그 수가 유한하다고 하더라도 전혀 현실적이지 못하다.
이러한 문제로 세상을 객체들의 집합과 이들 간의 관계 등을 표현할 수 있는 언어인 서술 논리(Predicate Logic)를 사용한다.
Example 1.

=> 경우의 수가 많아 객체들 간의 관계를 표현하기가 매우 어렵다.
* Predicate Logic Syntax
- Terms denote objects
· constant term: 고유한 명사 term
· variable term: 객체들을 가리키는 변수 term
· function term: 함수를 통해 객체를 가리키는 term

서술 논리의 문법을 정의하기 위하여 먼저 Term을 정의한다. Term은 세상이 객체(Object)들로 구성되었다고 가정하면 이 객체를 가리키는(denote) 혹은 표현하는 언어의 일부이다. 이를 이용하여 추후에 문장(Formula)를 구성하게 된다.
Term은 3가지의 방법으로 사용된다. 첫째는 constant term으로, 예를 들어 John, Mary 등과 같이 세상의 객체인 John이라는 남자, Mary이라는 여자를 가리키는 의미로 사용할 수 있다. John과 Mary 앞의 정의 K 라는 집합에 원소가 될 수 있겠다.
두 번째 방법으로 변수(variable) term으로, 예를 들어 x, y, z 등을 변수 심볼이라 하면, 이 변수들은 앞의 정의에서 사용한 집합 V의 원소들이 된다. 변수 term 들도 세상의 객체를 가리켜야 한다. 예를 들어 변수 x를 John이라는 남자를 가리키게 할 수도 있고 Mary라는 여자를 가리키는 변수로 사용할 수도 있겠다.
마지막으로 함수(function) term이 있다. 물론 함수 term도 세상의 객체를 가리켜야 한다. 예를 들어 John의 아버지를 표현할 때 함수 term, father-of(John)로 표현할 수 있겠다. 물론 father-of(John)도 john의 아버지 객체를 가리킨다. 이때 father-of는 function symbol로 argument 1개를 갖는 함수 심볼로 앞의 정의 F 집합의 한 원소가 되며, 함수 f(x)의 뜻은 x의 아버지를 나타낸다. 이러한 함수를 1-place function이라고 한다.
함수의 argument도 반드시 term이어야만 한다. Term은 상수, 변수, 함수 term이 되므로 재귀적(recursive)으로도 사용할 수 있다. 예를 들어 John의 아버지의 아버지는 father-of(father-of(John))으로 표현할 수 있으며 이 함수 term은 John의 할아버지인 객체를 나타낸다.
* Predicate Logic Definition

서술 논리의 문장(Formula)는 객체와 객체의 관계를 표현하는데 사용되며, 이러한 관계를 나타내는 심볼을 Predicate symbol이라고 한다. 예를 들어 John이 Mary를 사랑(loves)한다면 loves(John, Mary)로 표현 할 수 있는데 John과 Mary는 상수 term이고, loves는 2개의 argument(term)를 갖는 2-place predicate symbol이다. 이 때 loves는 앞에서 정의 한 집합 P 의 원소가 된다.
여기서 함수(function) term과 혼동하지 말아야 할 것은 predicate는 서술 논리의 문장인 formula를 만들며 John과 Mary의 관계, 즉 John이 Mary를 사랑하는 관계를 나타내며, 이 문장은 참일 수도 거짓일 수도 있다. 반편 함수 term, 예를 들어 father-of(John)은 객체를 나타내어 predicate의 argument 혹은 function의 argument로 사용되므로 관계를 나타내는데 사용될 수 없다. 만약 어떤 사람이 Smith가 John의 아버지라는 관계를 말하고 싶다면 관계를 나타내는 predicate, 예를 들어 2-place predicate symbol is-a-father-of를 사용하여 is-a-father-of(Smith, John) 표현할 수 있겠다.
Predicate symbol을 이용하여 표현한 서술 논리의 formula를 atomic formula라고 한다. 이러한 formula를 명제 논리에서 사용한 논리 연산자 ¬, ∨, ∧, ⇒, ⇔를 사용하여 복합(compound) formula를 만들 수 있다.
서술 논리에서는 이외에도 2개의 quantifier(한정사)인 universal quantifier와 existential quantifier를 사용할 수 있다. 전자는 모든 것(객체에) 대하여 관계가 성립함을 나타내며, 후자는 관계를 만족시키는 것(객체)이 존재한다, 즉 1개 이상 있다는 것을 나타낸다.
Example 3.

=> 위에서 Ontology 를 나타내는데 Constant term과 2-place predicate symbol을 가지고 formula를 정의할 수 있다.
loves(John, Mary)는 객체를 가리키는 Function term이 아니라 관계를 가르키는 2-place predicate symbol이다.
* 서술 논리 문장(formula)을 표현하는 방법
서술논리에서 사용되는 모든 심볼은 중복해서 사용할 수 없다. 그러므로 지식을 formula로 바꿀 때 먼저 ontology를 정의하고 사용하는 것이 좋겠다. 다만 변수(variable)는 일반적으로 x, y, z, p, q, r, s, t, u, v 등과 같이 한 개의 알파벳을 사용하고 한정사(quantifier) 하에서 사용되므로 (이러한 formula를 first-order sentence or closed formula라고 부른다) 혼동이 없으면 특별히 따로 정의하지 않고 사용하려고 한다.
=> Ontology 정의 예로, 상수(constant), function 심볼, predicate 심볼 등 정의하여 사용하는데, function 심볼과 predicate 심볼은 몇 개의 argument term을 갖는지 그 뜻을 표시해야 한다. 예를 들어: 2-place predicate symbol은 loves(x, y): x loves y로 표현 가능하다.
Example 4.

앞에서 언급했듯이 argument는 term이며 객체를 나타낸다.
따라서 function term도 객체를 나타낸다. 그러나 predicate 심볼은 관계를 나타내는 심볼로 formula를 표현할 때 사용된다. 따라서 predicate symbol은 formula의 term으로 사용될 수 없다.
위 예 Tweety is a bird에서 bird를 constant라고 한다며 세상에는 하나의 새(객체)만이 존재하게 되므로 우리가 표현하려는 뜻과는 거리가 있다. 따라서 bird를 1-place predicate symbol로 사용하는 것이 보통이다. 이렇게 1-place predicate symbol은 새들의 집합으로 볼 수 있다. 마치 class의 개념으로 한 개의 객체인 instance와 구분된다. 서술 논리의 의미론에서 predicate symbol은 집합의 의미를 갖고 있다. 반면 term은 한 개의 객체를 의미한다. 따라서 formula의 term으로 predicate symbol이 사용되면 이는 집합을 객체로 간주하게 되고, 이는 1st-order logic이 아닌 2nd -order가 되고 집합의 집합을 객체로 인정하여 3rd-order가 된다. 2 nd -order 이상을 high-order라고 부르며, 이 경우 의미론이 잘 정립되지 못한다.
Formula bird(Tweety)에서 1-place predicate symbol bird는 새들의 집합이고, Tweety는 그 집합에 속하는 하나의 새(객체, 원소)이다.
Formula ∀x bird(x) ⇒ canfly(x)에서는 universal quantifier(한정사)가 사용되었다. 뜻은 x가 새면 x는 날 수 있다라는 뜻으로 해석할 수 있겠다. 한정사 옆에 변수 x가 있는데 이를 직역하면 모든 x에 대하여 다시 말하면 x에 모든 객체를 대입해서 생각할 수 있으므로 x는 세상에 있는 어떤 한 개의 객체에 대하여 x가 새라면 x는 날 수 있다는 의미가 된다.
세상에 있는 모든 새가 날 수 있다는 뜻을 서술 논리에서 세상에 있는 각각의 새가 날 수 있다고 표현하고 있다.
같은 의미이지만 안에 있는 formula를 괄호를 써서 표현하면 ∀x (bird(x) ⇒ canfly(x)) 로 표시할 수 있다. 한정자의 scope가 하나의 문장(formula)에 미친다는 것을 알 수 있다.
Example 5.

지식을 서술 논리로 표현하는 방법은 어떤 문제를 풀 것이냐 에 따라 ontology를 정의하는 방법이 달라질 수 있다. 또한 지식이 앞으로도 계속 늘어날 것을 감안하면 더욱 세심하게 주의하여 ontology를 정의해야 한다. 따라서 단순히 영어 한 문장을 주고 이 것을 서술 논리 문장으로 바꾸라는 것은 옳지 않을 수 있다.
위 예는 existential quantifier를 사용한 예이다. 문제에 따라 ontology를 구체적으로 정의하여 표현할 수 있다. 예를 들어 영어 문장에 단순히 우리 반에 스파이가 있다는 내용으로 되어 있지만, 우리 반에 스파이는 사람 혹은 학생 등의 지식을 추가하여 표현 할 수 있지만 어떤 문제를 풀기 위한 문장인지 명확하지 않아 사람, 학생 등은 생략할 수도 있겠다.
Example 6.

=> 위의 예 에서 첫번째 formula는 새는 날 수 있다는 의미에 가깝지만,
두번째 formula ∀x bird(x) ∧ canfly(x) 의 의미는 세상에 모든 것은 새이고 날 수 있다 라는 뜻으로 해석되어 틀렸다고 말할 수 있다.
Example 7.

There is a baker who likes all of his customers.
∃x baker x ∧ ∀y customer(y) ⇒ likes(x, y)
How about?
∃x baker x ∧ ∀y customer(y) ∧ likes(x, y)
What it means?
It means there is a baker and every one is a customer,
and he/she likes the baker???
=> 이 세상의 모든 사람들이 그 baker를 좋아하는게 아니므로 맞지 않는 표현이다.
추가 예제
· ∀x customer(x)⇒likes(bob,x) :Bob likes every customer
· ∃x customer(x)∧likes(bob,x) :There is a customer whom bob likes
· ∀x older(mother(x),x) :Every mother is older than her child
· ∀x older(mother(mother(x)),x) :Every grandmother is older than her daughter’s child
· ∀x ∀y ∀z rel(x,y) ∧ rel(y,z)⇒rel(x,z) :rel is a transitive relation
Example 8.

=> 이 세상에 cake가 단 하나만 존재하지 않으므로,
위에서 constant term으로 정의한 것은 잘못되었다.
Example 9.
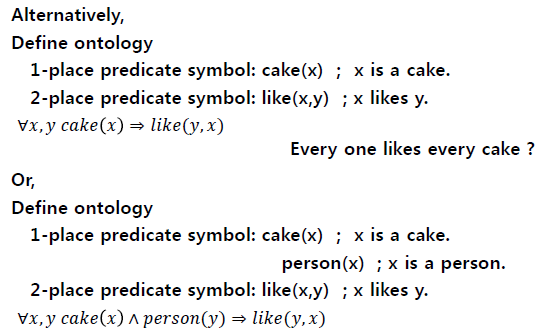
=> ∀x,y cake(x) ⇒ like(y,x) 는 "모든 사람이 모든 종류의 케잌을 좋아한다." 는 이야기로 표현되기 때문에,
∀x,y cake(x) ∧ person(y) ⇒ like(y,x) 로 표현하는 것이 "모든 사람은 케잌을 좋아한다." 말과 어울린다.
Example 10.

Example 11.

=> KB = {∀x man(x) ⇒ mortal(x), man(Socrates)} 일 경우
KB |= mortal(Socrates) ? 답은 yes.
man(Socrates) ⇒ mortal(Socrates) ≡ ┐man(Socrates) ∨ mortal(Socrates)
따라서 ┐man(Socrates) 가 false이기 때문에 mortal(Socrates) is true가 된다.
위에서 설명된 내용은 모두 집합이라고 보고 이를 집합에 의한 의미론이다 하여 Set theoretic Semantics 혹은 객체를 가리킨다 하여 Denotation Semantics 이라고 불리기도 한다.
* Semantics (의미론)

서술 논리의 의미론을 정의하기 위하여 interpretation B를 먼저 각 term들에 대하여 정의한다.
K ∪ V 에 속한 상수와 변수 term은 정의하려는 세상(world)에 있는 객체로 mapping 된다.
이 때 세상에 있는 모든 객체들의 집합 W 를 universe of discourse라고 부른다.
Interpretation B를 function 및 predicate symbol에 대하여도 정의하면 서술 논리의 의미론이 완성된다.
본 책에서는 이에 대한 정의를 수학적으로 완벽하게 정의하고 있지는 않지만, 그 의미를 설명하는 형식으로 정의하였다.
N-place function symbol은 세상에 있는 n-place function으로 mapping한다고 정의하였다. 세상에 있는 function은 무엇일까? Function은 n개의 입력 파라미터로 부터 하나의 함수 값(객체, object)을 갖는 mapping이다. 예를 들어 누구의 아버지를 함수로 생각할 수 있다. Sin, cos 함수도 생각할 수 있다.
N-place predicate symbol은 세상에 있는 n-place 관계로 mapping 한다고 정의하였다. 예를 들어 “누가 어떤 사람을 때렸다”라는 두 사람간의 관계 혹은 사실을 표현하는 문장으로 그 문장이 참 혹은 거짓으로 mapping하는 의미론으로 정의하였다.
* Definition

· Atomic formula P(t 1 ,t 2 ,...,t n )의 의미, 즉 B(P(t 1 ,t 2 ,...,t n ))는 참 아니면 거짓인데, 이 값은 집합론적으로 다음 관계가 의하여 성립하면 참이고 아니면 거짓이 된다: (B(t 1 ), B(t 2 ), ..., B(t n )) ∈ r, 여기서 r은 predicate P가 표현하는 세상의 n-place relation(관계)이다. 예를 들면 사랑(love)하는 관계이다. 보다 자세한 예는 후에 더 제시하도록 하겠다.
· 나머지 논리 연산자인 ¬, ∧, ∨, ⇒, ⇔를 포함하는 formula의 참값의 정의는 명제 논리에서 정의한 것과 같다.
· 새로 추가된 한정사 ∀x F는 formula F에 나오는 변수 x에 대하여 모든 B(x), 즉 모든 객체에 대하여 F가 참이 된다.
· ∃x F는 formula F에 나오는 변수 x에 대하여 적어도 하나의 객체 B(x)가 F를 참으로 하는 것이 존재한다.
· 서술 논리에서도 formula에 대한 statifiability, validity, unsatisfiability, model 등의 용어는 명제 논리에서 정의한 것과 통일하게 사용될 수 있다.
* Satisfiability (만족 가능성)

=> 명제 논리와 Satisfiability 조건이 동일하다.
Example 12.

=> B1의 경우 결과 값인 (4,2) 가 G에 포함되므로 F는 True 이지만,
B2의 경우 결과 값인 (1,3)은 G에 포함되지 않아 F는 False 이다.
* Extended definition of logical entailment
Example 13.

=> 명제논리와 동일하게 서술논리에서도 entailment 를 정의 가능하다.
Example 14.
서술 논리로 지식을 표현 방법을 아래에 나오는 가족 관계 트리 문제로 더 생각해 보자. 이를 위하여 먼저 ontology를 정의해야 한다. 많은 사람 이름들이 상수 term들이 되고 필요에 따라서 predicate symbol을 정의할 수 있겠다. 예를 들어 다음과 같이 2개의 predicate symbol을 정의했다고 하자. 1-place predicate female(x): x is a female 3-place predicate child(x, y, z): x is a child of y and z
다음 가족 트리에서 Karen은 여자이고, Oscar A.는 karen과 franz의 아이이다는 표현을 다음과 같이 서술 논리 formula로 표현할 수 있겠다: female(karen), child(oscar A. karen, franz). 이 때 본 책에서는 소문자 karen은 서술 논리에서 사용하는 상수 symbol이고, 대문자 Karen 세상에 있는 객체 Karen을 나타내기 위하여 구분하였다.

=> 컴퓨터는 우리가 지식을 넣어주지 않으면 일반적인 상식선에서 알지 못하는 지식이 존재한다.
따라서 위의 지식베이스에서 두개의 지식이 추가되었다. 하나는 child(x, y, z)의 관계에서 y와 z가 바뀌어도 관계는 성립하기 때문에 지식을 추가하였고,
descendant(x, y)는 “x는 y의 후손”이라는 관계를 표현하기 위해 2-place predicate symbol을 추가하였다.
이는 주어진 문제에 따라 지식을 늘릴 수 있겠다.
이 정의에는 x가 y의 후손이 되는 경우는 x가 y의 아이(child)이거나 재귀적(recursive)으로 x가 y 후손의 아이인 경우로 정의하였다.

=> 서술 논리에서도 명제 논리처럼 entail하는지 계산할 수 있는 derivation 프로그램인 theorem prover가 필요하다.
이를 위하여 궁극적으로 resolution-refutation 방법을 사용하기 위하여는 먼저CNF(Conjunctive Normal Form)으로 변환하여 한다.
이를 위하여 서술 논리에서는 명제 논리에 없는 한정사를 제거하는 과정이 필요하다.
이를 위하여 prenex normal form으로 먼저 만들고, existential quantifier를 skolemization을 이용하여 제거하고 최종적으로 universal quantifier 제거하게 된다. 또한 unification process도 필요하다. 이는 추후에 배우기로 한다.
* Equality
서술 논리에서 term을 사용하여 객체를 나타내게 되는데 우리 종종 같은 객체를 다른 이름으로 사용하는 경우가 많다. 예를 들어 John’s father를 function term으로 father-of(john)이라고 표현할 수도 있지만, John’s father가 Smith라고 한다면, 우리는 쉽게 father-of(john) = smith라는 관계를 표현 할 수 있다.
이 때 = symbol을 어떻게 처리할 것인가 하는 문제가 생긴다. 한 가지 방법은 = symbol을 predicate symbol로 간주하는 경우이다 (물론 이 때 문법은 일반 predicate와 다르게 양쪽에 term이 오는 형식으로 2-place predicate symbol이다). 이럴 경우 = symbol은 다음 슬라이드에 나오는 것같은 axiom이 필요하게 된다.
다른 한가지 방법은 = symbol을 특수 연산자로 정의하여 사용할 수 있지만 이는 구현(control)의 방법으로 해결하는 것으로 순수한 논리 언어라고 볼 수 없겠다. 어쨌든 논리 equality 심볼은 많은 문제점을 내포하고 있어 지식표현 시스템에서도 equality 사용을 불허하는 경우도 있다.

Example 15.

=> John's father와 Smith는 동일 인물로 Equality axioms의 예이다.
* Term Substitution(치환 실례)

=> 변수를 term으로 대체(substitution) 할 수 있다.
예를 들어, ∀𝑥 𝑏𝑖𝑟𝑑 𝑥 ⇒ 𝑐𝑎𝑛𝑓𝑙𝑦(x) ∧ 𝑏𝑖𝑟𝑑(𝑡𝑤𝑒𝑒𝑡𝑦) 이 경우 변수 x에 term tweety를 대체 시킨 formula 𝑐𝑎𝑛𝑓𝑙𝑦 𝑇𝑤𝑒𝑒𝑡𝑦 도 참이 된다.
=> 대체 시키는 term에 그 변수를 포함 후 대체시키면 잘못된 결과가 초래된다.
Example 16.
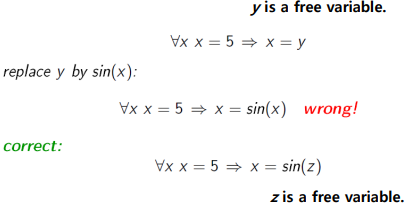
=> 위 경우 sin(x)에서 x가 겹치지 않도록, z로 rename을 시켜야 한다.
* Quantifiers and Normal Forms

=> universal quantifier는 conjunction의 의마가 존재하고,
existential quantifier는 disjunction의 의미가 존재한다.
=> 서술 논리 formula를 CNF로 만들기 위하여 먼저 prenex normal form 을 만들고
skolemization process를 통해 existential quantifier를 제거 하고 최종적으로 universal quantifier을 제거하게 된다.
추가 예제
· Ontology 1-place predicate loved(x): x is loved
· Everyone wants to be loved. ∀𝑥 𝑙𝑜𝑣𝑒𝑑 𝑥 ≡ ¬∃𝑥 ¬𝑙𝑜𝑣𝑒𝑑(𝑥)
· No one wants to be loved. ¬∃𝑥 𝑙𝑜𝑣𝑒𝑑 𝑥 ≡ ∀𝑥 ¬𝑙𝑜𝑣𝑒𝑑(𝑥)
=> ∀𝑥 α ≡ ¬∃𝑥¬ α로 변환 가능
=> ¬∃𝑥 α ≡ ∀𝑥¬ α로 변환 가능
Example 17.

=> Ontology:
Constant symbol: 0, b, N
Function symbols: abs(x) ; 𝑥 a(n) ; 𝑎𝑛 minus(x, y) ; 𝑥 − 𝑦
Predicate symbols: el(x, y) ; 𝑥 ∈ 𝑦 gr(x, y) ; 𝑥 > 𝑦
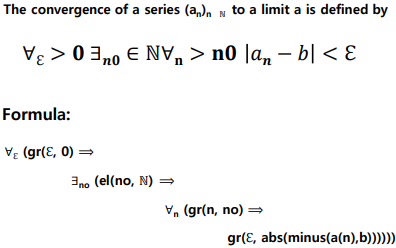
Example 18.

=> 모든 predicate logic formula는 quivalent formula in prenex normal form 으로 변환 될 수 있다.
prenex normal form은 quantifier가 모두 앞으로 빠진 형태이다.
* Elimination implications

=> 함축 제거 (Implication Elimination)는 그 함축과 그 선행으로부터 함축의 결과를 추론 할 수있는 추론의 규칙입니다.
아주대학교 정보통신대학원 김민구 교수님의 인공지능 강의를 바탕으로 작성하였습니다.
학습 목적으로 포스팅 합니다.
'Artificial Intelligence' 카테고리의 다른 글
| Limitations of Logic (0) | 2020.09.30 |
|---|---|
| 서술논리 ② (0) | 2020.09.25 |
| 명제논리 (2) | 2020.09.12 |